StatQuest 머신러닝 강의 정리

안녕하세요 머킹입니다.
드디어 이 책을 완독 했습니다.
개인적으로 이 책을 정리해서 블로그에 적으려고 했는데 책이 대부분 그림이라
빌려서 보시는 게 좋을 것 같습니다.
https://www.youtube.com/@statquest
StatQuest with Josh Starmer
Statistics, Machine Learning and Data Science can sometimes seem like very scary topics, but since each technique is really just a combination of small and simple steps, they are actually quite simple. My goal with StatQuest is to break down the major meth
www.youtube.com
유튜브도 있는데 되게 재밌게 설명해 주셔서 흥미로워서 책을 읽게 됐어요.
노래로도 알려주시고 보다 보면 되게 재밌어요.
아무튼 간략하게 정리한 것들을 올려보겠습니다.
머신러닝이란?
데이터를 의사결정으로 변환해 주는 도구와 기술의 집합
분류(Classification) : 어떤 사람이 특정 영화를 좋아할지 여부
예측(Regression) : 사람의 키와 같은 정량적 예측
- 어떤 것을 분류하거나
- 양적 예측을 하는 데 사용
테스트 데이터와 훈련 데이터를 나눠서 머신러닝을 평가한다.
머신러닝 방법이 훈련 데이터에 잘 피팅되었다고 해서
테스트 데이터에도 반드시 좋은 성능을 내는 것은 아니다.
과적합
훈련 데이터에서는 높은 수치가 나오지만 예측 시에는 좋은 성능을 보여주지 못하는 것
독립 변수와 종속 변수
💡 변수 : 변하는 값
종속 변수 : 독립 변수에 의존
독립 변수 : 종속적이지 않는 변수
예시
몸무게 키
| 0.4 | 1.1 |
| 1.2 | 1.9 |
- 여기서는 몸무게의 정보를 알고 키를 예측하기 때문에
- 키 : 종속 변수
- 몸무게 : 독립 변수, feature라고도 함
여러 개의 독립 변수 혹은 특징을 사용해도 됨
이산형 데이터(discrete data)
- 셀 수 있으며 특정 값을 가지는 데이터
- ex) 순위나 다른 순서들 1등, 2등, 3등 순으로 상을 가져감 (1.64등은 존재 x)
연속형 데이터(continuous data)
- 측정할 수 있으며 범위 내의 어떤 수치 값이든 가질 수 있음
- ex) 사람의 키는 0과 큰 누군가의 키 사이의 어떤 숫자든 가능함
교차검증(cross validation)
- 훈련 데이터와 테스트 데이터가 구분되지 않으면 교차검증을 통해 편향(bise) 없는 방법을 찾음
- 교차검증은 모든 데이터를 훈련과 테스트에 모두 반복 적용 (반복 시행 횟수 : 폴드)
데이터 누수 : 훈련에 사용한 데이터를 테스트에 재사용하는 것
- 반복 테스트 결과를 통해 오차 값들의 평균을 짐작할 수 있음
💡 데이터가 많을 경우 일반적으로 10-폴드 교차검증을 사용함
- 데이터 순서를 임의로 섞기
- 데이터를 10개의 동일한 사이즈 블록으로 랜덤 하게 나누기
- 처음 9개 블록을 훈련에 사용하고, 10번째 블록을 테스트에 사용
💡 리브-원-아웃(leave-one-out) - 데이터셋이 매우 작을 경우
- 하나의 데이터를 제외하고 모두 훈련에 사용
- 남은 하나의 데이터를 테스트에 사용
- 모든 데이터 포인트가 테스트에 사용될 때까지 반복
통계(statistic)
- 발견하는 변화를 정량화할 수 있는 일련의 도구 제공
- 머신러닝의 목적인 예측과, 그 예측의 신뢰도 파악
[히스토그램]
- 값의 범위를 구간으로 나누어주고, 같은 구간에 들어오는 측정값을 쌓음
- 구간의 크기를 잘 결정해야 함

확률분포(distribution)
- 가진 데이터가 많지 않다면 히스토그램으로 확률을 예측하기 어려움
- 히스토그램을 근사하는 종모양의 확률분포를 나타냄
이산확률분포(discrete distribution)
- 데이터를 이산 구간에 넣을 수 있고 이를 통해 확률을 예측
- 이항분포 (binomial distribution)

x = 호박 파이를 선호하는 사람의 숫자
p = 확률
수직선, 혹은 파이프 기호(|) : 어떤 조건이 주어졌다
팩토리얼(factoria,!) : 정수 숫자와 그 아래의 모든 양의 정수의 곱
ex) 3! 는 3 x 2 x 1 = 6
“파이 선호도를 물어본 n=3명 중 어떤 사람이 호박 파이를 좋아할 확률이
p = 0.7일 때, x=2명이 호박 파이를 좋아할 확률”
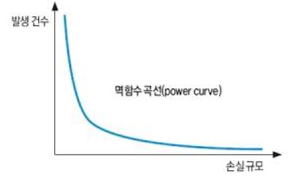
푸아송 분포(poisson distribution)
- ‘1시간에 10페이지 읽기’처럼 이산형 시간 단위, 혹은 공간 단위에서 발생하는 사건이 존재
람다 (λ) : 평균
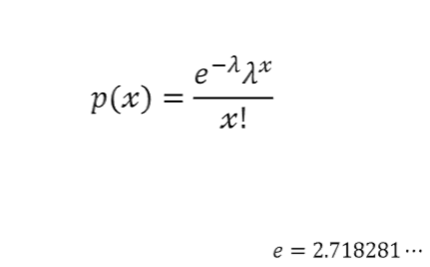
정규분포(Gaussian distribution)
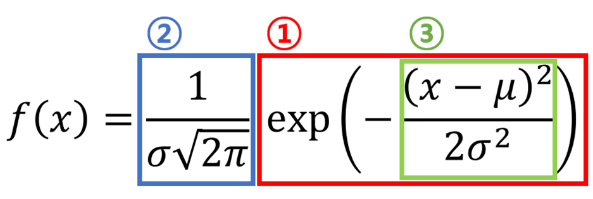
- 평균, 혹은 상술평균 기댓값에 대해 대칭인 분포
- 정규분포의 너비는 표준편차(standard deviation)에 의해 결정됨
- 그리는 방법
- 측정값의 평균 혹은 산술평균. 곡선의 중심이 어디에 위치해야 하는지 알려준다.
- 측정값의 표준편차. 곡선의 모양이 높아야 하는지 짧아야 하는지 등을 알려준다.
- 공식의 최종결과인 좌푯값은 우도(혹은 가능도)며 확률이 아니다.
ex : 키, 출생 시 몸무게, 혈압, 근무 만족도 등등에 사용
💡 지수 분포(exponetial distribution)
- 이벤트 사이에 지나간 시간을 살펴볼 때 사용
균일 분포 (uniform distribution)
- 일어날 확률이 같은 난수를 생성하는 데 사용
모델 : 주요 개념
- 머신러닝 모델은 다양하게 사용할 수 있는 현실에 대한 근삿값을 제공
- 머신러닝에서 훈련 데이터로 머신러닝 알고리즘을 훈련시켜 모델을 제작
- 통계는 모델이 유용한지 혹은 믿을 만한지 결정하는 데 사용
잔차제곱합
잔차 = 관측값 - 예측값
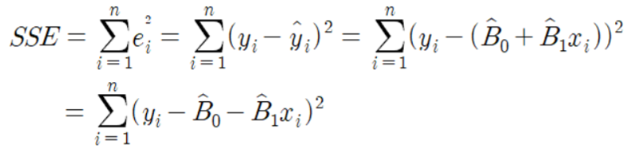
모든 관측값과 예측값 사이의 거리를 제곱한 값의 합
n = 관측값 개수
i=1 : 관측값의 인덱스
시그마 : 합(summation)
평균제곱오차(MSE) (잔차 제곱합의 평균)
= 잔차제곱합(SSR)/관측값 개수(n) = nΣi=1 (관측값 i-예측값 i) 2 / n
더 많은 데이터를 가질수록 더 많은 잔차를 갖게 됨
- 크기가 다른 데이터셋에 피팅된 두 모델을 비교하기 위해서 평균제곱오차를 계산해야 함.
R^2
- 잔차제곱합 혹은 평균제곱오차를 비교해 계산함
- 단순히 평균을 계산하는 것보다 모델을 사용해 예측했을 때 어느 정도 개선되는지 백분율 표시
P-값 : 핵심 개념
p-값(p-value)은 통계 분석 결과에 대한 신뢰도를 나타냅니다. (모델의 신뢰도 파악)
거짓 양성(false positive)
- 차이가 없는데도 불구하고 작은 p-값을 얻는 것
가설검정 (hypothesis test)
- 차이가 있는지 여부를 결정하는 아이디어
귀무가설(null hypothesis)
- 약의 효과가 같다는 뜻이고 p-값은 우리가 귀무가설을 기각할 수 있는 근거를 제공
선형회귀(linear regression)
- 선형모델(linear model)이라는 일반 기법의 관문.
- 선형모델은 단순히 직선을 데이터에 피팅하는 것을 넘어서는 방법
- 잔차제곱합을 가장 작게 만드는 y절편과 기울기를 가진 선을 선택하는 것
경사하강법
- 반복 솔루션으로 최적의 솔루션을 향해 점진적으로 나아감
손실함수/비용함수
- 모델을 데이터에 피팅할 때 최적화하려는 모든 것에 적용
- 손실 혹인 비용함수는 잔차제곱합이다.
- 도함수를 계산하면 미분값이 나옴
잔차제곱합
SSR = ( 키 - (절편 + 0.64 X 몸무게) ) 2
잔차제곱합을 잔차에 관한 함수로 다시 작성해 절편과 잔차제곱합 사이의 링크를 생성
**멱 규칙(the power rule)**을 활용해 미분을 해준다.
파라미터
- 최적화하고자 하는 것은 파라미터(parameter)
- 임의로 결정한다는 의미
- 단순히 각 단계에서 임의로 하나의 데이터 포인트를 선택하는 일

- 한계 : S자 곡선을 데이터에 피팅할 수 있다고 가정해야 한다는 점
확률 vs 우도(가능도)
확률과 우도는 다르다. 하지만 항상 다른 것은 아니다.
확률과 우도가 같은 경우에는 확률이나 우도를 사용해 곡선을 데이터에 피팅할 수 있다.
훈련 데이터셋이 커지면 계산할 때 언더플로 문제가 발생할 수 있음.
언더플로 : 0과 1 사이의 작은 숫자를 계속해서 곱할 때 발생.
오차의 원인이 되며, 더 좋지 않은 경우에는 예측하기 힘든 결과를 내놓기도 함.
나이브 베이즈
나이브 베이즈 알고리즘에는 여러 종류가 있지만 다항 나이브 베이즈를 가장 많이 사용
ex ) 스팸을 분류하자
‘친애하는 친구에게’라는 메시지가 정상 메시지인지 스팸인지 구별
- 8개의 정상 메시지와 4개의 스팸 메시지가 있는 훈련 데이터 사용
- 먼저 정상 혹은 스팸일 수 있는 메시지에 담긴 내용을 보지 않고 추측한 확률인 사전 확률을 계산
- 그다음 메시지에 담긴 각 단어의 히스토그램 생성
- 그리고 히스토그램을 사용해 확률을 계산
- 그 다음 메시지가 정상 혹은 스팸일 조건에 따라 사전 확률과 각 단어가 나올 확률로 ‘친애하는 친구에게’라는 메시지의 점수를 계산
- 이제 ‘친애하는 친구에게’라는 메시지를 분류할 수 있음
- 정상 메시지일 확률, 즉 점수는 0.99로 해당 메시지가 스팸일 점수보다 크기 때문에 우리는 이 메시지를 정상 메시지를 구분함
나이브 베이지라는 명칭에서 나이브라는 모든 단어를 단순하게 독립적으로 취급하기에 붙여짐
훈련 데이터가 충분히 크지 않다면 결측치를 갖기 쉽다.
- 따라서 나이브 베이즈는 결측치 문제를 각 단어에 대한 근사수(혹은 가짜 빈도수)를 추가하는 방법으로 제거
- 근사수란 각 단어에 더해지는 추가 값
모델 성능 평가하기
혼동 행렬(confusion matrix)
- 로지스틱 회귀 / 나이브 베이즈 중에서 고르기
- 데이터와 결괏값에 대해서 살펴보고 맞는 것을 고를 것(정답은 없다)
민감도와 특이도
- 민감도란 실제 양성이 정확히 분류된 비율
- 특이도란 실제 음성(심장병이 없는 사례) 사례가 정확히 분류된 비율
Accuracy
정확도는 말 그대로 얼마나 정확하냐를 측정하는 지표이다. 예를 들어, 개와 고양이를 분류하는 모델에서 전체 (개 5장, 고양이 5장) 10장 중 9장을 올바르게 분류하고 1장을 다르게 분류했다면 해당 모델의 정확도는 90%가 된다. 이를 보다 정확하게 표현하면 아래와 같은 그림이 된다. (# = the number of = ~의 수)

정확도는 분류 문제에서 클래스들이 동일한 분포를 갖고 있을 때 유용하게 쓰인다. 쉽게 말해 개의 사진이 100장 고양이 사진이 100장 있다면 equal distribution이라고 할 수 있다.
Precision: the first part of the F1 score
Precision은 독립적인 메트릭으로도 사용될 수 있다. 공식은 아래와 같다.

이것을 해석하자면, 모델이 True라고 분류한 것 중에서 실제로 True인 것의 비율이다.
- 정확하지 않은 모델은 많은 것을 positive라고 예측할 것이다. 하지만 negative인 것을 positive로 예측한 노이즈가 많이 껴있을 것이다.
- 정확한 모델은 "pure", 즉 순수하다. 모든 positive를 찾지는 못하더라도 최소한 positive라고 예측한 것은 모두 positive인 것을 의미한다. 쉽게 말해, 암에 걸렸다고 판단한 데이터가 100명이라면 100명 모두 실제로 암에 걸린 것이다.
Recall: the second part of the F1 score
Recall 또한 독립적인 메트릭으로도 사용할 수 있다. 공식은 아래와 같다.

이것을 해석하자면, 실제 True인 것 중에서 모델이 True라고 예측한 것의 비율이다.
- Recall이 높으면 몇 개의 negative를 positive로 분류할지라도 data에서 positive case를 잘 찾은 것을 의미한다.
- Recall이 낮으면 데이터에서 positive case들을 전혀 찾을 수 없다는 것이다.
Precision vs Recall
그래서 뭐가 어떻게 다를까? 명백히 하자면, 슈퍼마켓에서 문제가 있는 제품을 팔았을 때, 그들은 문제가 있는 제품들을 회수(recall)하고 싶을 것이다. Precision과 Recall의 차이는 분모에 FP가 들어가냐 FN이 들어가냐 이다. 여기서 True positive, True Negative, False Positive, False Negative를 알아보자.

- True positive: 문제가 있는(positive) 제품을 문제가 있다고(positive) 잘(true) 판별한 것.
- True Negative: 문제가 없는(negative) 제품을 문제가 없다고(negative) 잘(true) 판별한 것.
- False Positive: 문제가 없는(negative) 제품을 문제가 있다고(positive) 잘못(false) 판단한 것.
- False Negative: 문제가 있는(positive) 제품을 문제가 없다고(negative) 잘못(false) 판단한 것.
그들은 오직 문제가 있는 모든 제품을 다시 되돌려 받는 것에만 관심이 있고 몇 클라이언트가 문제가 없는 제품을 되돌려주어도 상관이 없다면 precision은 이 슈퍼마켓의 관심사가 아닌 것이다.
민감도, 특이도, 정밀도, 재현율 노래
- 민감도는 정확히 예측된 참 양성 비율이야
- 특이도는 정확히 예측된 참 음성 비율이야
- 정밀도는 조금 달라. 정밀도는 정확히 예측된 양성 비율이야
- 그리고 재현율은 다시 처음으로 돌아가 민감도와 같지
ROC 그래프
- 좋은 분류 임계값을 찾고자 할 때 큰 도움
- 참 양성 비율과 거짓 양성 비율 관점에서 각 임계값이 얼마나 좋은 성능을 내는지 한 번에 요약
AUC(area under the curve) 곡선 아래면적
- 모델 성능 비교
정규화
훈련 데이터 과적합을 다루는 가장 흔한 방법은 정규화라는 기술을 사용하기
정규화는 훈련 데이터에 대한 모델의 민감도를 줄여준다.
정규화는 편향을 소폭 증가시키지만 분산을 대폭 줄인다.
릿지 정규화
릿지 페널티는 절편을 포함하지 않는다.
절댓값을 태움
리쏘 정규화
제곱값을 태움
가장 적절한 가중치를 찾아서 맞은 만큼 틀렸다고 하는 것 (즉, 불순물을 태우는 것)
실전파 모델을 만들기 위해서
리쏘와 릿지는 상황에 따라 더 유용한 것을 사용한다.
의사결정 트리
- 머신러닝에는 분류, 회귀 트리가 있음
- 분류 트리 : 카테고리로 분류
- 회귀 트리 : 연속형 값을 예측
트리 상단은 루트 노드, 혹은 루트라고 부름
분류 트리
여러 분류가 섞여 있는 리프를 불순하다고 부름
트리와 리프의 불순도를 정량화하는 방법으로는 지니 불순도를 많이 사용
엔트로피와 정보이득 등의 방법도 있음
총 지니 불순도 = 모든 리프의 지니 불순도 가중평균
서포트 벡터 머신
- 데이터에 새로운 축을 추가해 분류를 정확히 할 수 있는 직선을 상대적으로 쉽게 그릴 수 있도록 점들을 이동시킵니다.
- 이상한 중간점을 사용하면 이상치에 영향을 받습니다.
- 분류 임계값을 이상치에 더 민감하도록 만드는 한 가지 방법은 오분류를 허용하는 것
- 임곗값과 임곗값 자체를 정의하는 점 사이의 거리를 마진이라 합니다
- 오분류를 허용할 때 해당 거리를 소프트 마진이라고 부릅니다.
점복에 의해 계산된 관계는 경사 하강법과 같은 라그랑주 승수법이라는 기법의 입력으로 사용됨
라그랑주 승수법은 경사 하강법처럼 한 번에 한 단계씩 최적의 서포트 벡터 분류기를 찾는 반복적인 방법임.
신경망
신경망은 층으로 구성됨
일반적으로 신경망은 입력층을 구성하는 여러 개의 입력 노드가 있음
그리고 출력층을 구성하는 출력 노드가 있음
입력과 출력 사이의 노드를 은닉층이라고 함
활성화함수는 데이터에 피팅하기 위한 기본 토대가 됨
대표적으로 ReLU, 소프트플러스, 시그모이드를 사용함
신경망은 늘리고, 회전시키고, 자르고 추가로 활성화 함수를 결합해 어떤 데이터에도 피팅할 수 있는 새롭고도 흥미로운 모양을 만들어냄
역전파
- 선형회귀처럼 신경망에도 데이터에 구부러진 선을 피팅하기 위해 최적화해야 하는 파라미터가 존재함
- 최적값을 찾기 위해서 경사 하강법 혹은 확률적 경사 하강법을 사용할 수 있음
- 우리는 이를 신경망에서 각파라미터들의 미분값을 찾는 역전파를 사용함
- 가중값(weight) : 신경망에서 곱하는 파라미터들
- 편향 (bias) : 더하는 파라미터들
- 마지막에 역전파를 사용해 마지막 편향을 최적화를 할 것
이렇게 길고 긴 책이 끝났는데요.
진짜 동화책처럼 그려져 있는 게 많아서 이렇게 글로 정리하기가 더 애매했지만
그래도 머신러닝을 다시금 또 상기시켜서 재밌었습니다.
유튜브에 논문도 읽으시는데 그게 되게 재밌어요.
앞에 노래가 되게 중독돼서 노래 듣는 재미가 있달까요..
가끔 이렇게 책 정리할 수 있으면 해 보겠습니다.
'AI > 머신러닝' 카테고리의 다른 글
| 머신러닝 개발자는 어떤 언어가 필요할까 (0) | 2023.07.29 |
|---|---|
| 머신러닝은 대체 무엇인가? (1) | 2023.07.28 |
| 머신러닝 초보자 꿀팁 사이트 모음 (2) | 2023.07.27 |
| 머신러닝 무료 강의 추천[도움 되는 사이트 정리] (1) | 2023.07.26 |
| 머신러닝 개발자의 첫 시작 (0) | 2023.07.25 |

